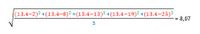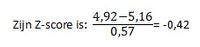STATISTIEK
METEN IS WETEN (deel 1)
Door Maarten Groot
Militairen moeten onder alle klimatologische omstandigheden fysieke uitdagende werkzaamheden uit kunnen voeren. Als LO&Sportorganisatie zorgen wij voor fysieke fitheid en mentale weerbaarheid, essentieel voor gezond en inzetbaar personeel van de Koninklijke Landmacht. Maar wanneer zijn de militairen die wij trainen nou fysiek fit? Wanneer wordt de militair sneller, sterker of meer wendbaar? Hoe stel je reële doelen voor de komende trainingsperiode? Hoe maak je vooruitgang inzichtelijk? Hoe herken je talent of aanleg? Wanneer is een trainingsperiode effectief geweest? Met een serie van 3 artikelen gebaseerd op hoofdstuk 13 uit ‘Essentials of Strength Training and Conditioning’ hoop ik inzicht te geven in mogelijke manieren om antwoord te kunnen geven op bovenstaande vragen.
In dit deel wordt beschrijvende statistiek, variabiliteit en normaalverdeling besproken. In deel twee wordt gekeken naar wanneer een verandering in prestatie relevant is. In het laatste deel worden een aantal praktische voorbeelden gegeven hoe Excel 2016 gebruikt kan worden voor snelle verwerking van data naar informatie.
De eerste stap naar antwoorden op de eerder genoemde vragen is het opstellen van een sport- of motorische test, of een combinatie van testen die samen een testbatterij vormen. Voorbeelden van een testbatterij bij Defensie zijn de Defensie Conditie Proef (DCP) maar ook de Algemene Militaire Fitheid (AMF) test. Het opstellen van een testbatterij valt buiten de doelstelling van dit artikel. In de onlangs uitgebrachte doctrinepublicatie LAND-E&T-LO&S-00 “Handboek Militairy Strength & Conditioning” wordt in hoofdstuk 10 uiteengezet waar een goede test of testbatterij aan moet voldoen.
Als er inmiddels een goede test of testbatterij is geselecteerd en de resultaten zijn verzameld, zijn er een aantal vervolg stappen mogelijk.
1. De resultaten kunnen worden gebruikt om te zien of de prestatie van individuen of de groep als geheel zijn veranderd gedurende de trainingsperioden (weken, maanden of jaren). Bijvoorbeeld door in januari en juli de spronghoogte te meten.
2. Met de resultaten kan de individu of groep worden vergeleken met soortgelijke individuen of groepen. Bijvoorbeeld door de AMF-resultaten van GNK militairen in Havelte te vergelijken met de resultaten van GNK militairen in Oirschot. Of de resultaten van de Looptest Fysieke Voortzetting (LFV) van leerlingen op de KMS in 2021 vergelijken met de leerlingen KMS van voorgaande jaren.
3. Analyse van het verschil tussen de resultaten van het enkele individu ten opzichte van de hele groep. Voorbeeld: na een trainingsperiode met de focus op plyometrie is te zien dat de gemiddelde vertesprong van de groep met 2 cm is vergroot. Bij het bekijken van de individuele vooruitgang is te zien dat 1 individu 1 cm minder ver sprong. Het resultaat van deze valt dus buiten de verwachtte voortuitgang die de groep liet zien.
4. Als laatste kunnen resultaten worden gebruikt om de individuen te vergelijken met lokale, nationale of internationale normeringen. Bijvoorbeeld de resultaten van de 1RM bench press van een individu vergelijken met de 1RM resultaten van Nederlandse mannen in dezelfde leeftijdscategorie.
Een belangrijke uitkomst van herhaalde metingen is de evaluatie van zowel de vooruitgang van de sporters als de effectiviteit van het trainingsprogramma. Dat kan gedaan worden door het verschil tussen de metingen uit week 1 en week 14 te berekenen. Dit verschil zou verder omgerekend kunnen worden naar een procentuele verandering. Deze methode kent echter wel 2 beperkingen. De eerste is de wet van de verminderde meeropbrengst, waardoor er bij minder getrainde personen veel meer progressie zichtbaar is dan bij meer getrainde personen. Daarnaast zouden een aantal personen bij de eerste meting opzettelijk minder hun best kunnen doen, om zo bij de tweede meting beter te scoren. Zorg er dus altijd voor dat deelnemers bij een test altijd maximale inzet geven zowel op de nul- als nameting.
Beschrijvende statistiek
Statistiek is de wetenschap van het verzamelen, classificeren, analyseren en interpreteren van data. Na het uitvoeren van een test of testbatterij kan er worden gekeken naar hoe de resultaten van de groep zijn verspreid. Meest gebruikte methode hiervoor is om het gemiddelde te berekenen.
Naast het gemiddelde is het ook aan te raden om te kijken naar de spreiding van de data. Dat kan door het bereik inzichtelijk te maken, dus door de hoogste en de laagste score te bekijken. Of door de standaarddeviatie te berekenen. Voordeel van het bereik is dat deze makkelijk te begrijpen is. Nadeel is dat er uitschieters naar boven of naar onder bij kunnen zitten die het groepsbeeld vertekenen.
Voorbeeld: Om te weten te komen wat het kracht-uithoudingsvermogen in het bovenlichaam is van vrouwelijke militairen in de AMO heb je besloten een 2 minuten push up test uit te voeren. De resultaten van de deelneemsters zijn: 2, 8, 13, 19, 25.
De laagste en de hoogste score zijn 2 en 25. De standaarddeviatie wordt berekend door:
1. Van elk getal de afstand tot het gemiddelde te nemen;
2. Het kwadraat van die afstanden te nemen;
3. Het gemiddelde van die kwadraten te nemen;
4. Neem de wortel van deze uitkomst.
Een kleine standaarddeviatie geeft aan dat alle scores redelijk in de buurt komen van het gemiddelde. Een grotere standaarddeviatie geeft dus aan dat er een grotere spreiding is in de groep.
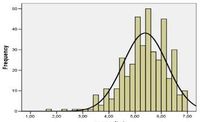
De standaarddeviatie is het meest zinvol als de verzamelde data “normaal verdeeld” is. Normaal verdeelde data ziet er in een histogram vaak uit als een klok, zie figuur 1. In een histogram worden overeenkomstige waarden (frequentie dat een waarde voorkomt) op elkaar gestapeld.
Figuur 1, histogram met normaalverdeling (zwarte doorgetrokken lijn)
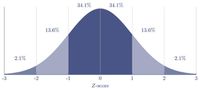
Een manier om aan te geven hoe de resultaten van een individuele militair zich verhouden tot het gemiddelde is om de Z-score te berekenen. Dat kan door het gemiddelde af te trekken van de score van de deelnemer en dit te delen door de standaarddeviatie. In figuur 2 is een weergave van Z-scores en percentages bij een normaal verdeling. Een Z-score van 1 of -1 betekent 1 of -1 standaarddeviatie van het gemiddelde, 2 of -2 betekent 2 of -2 standaarddeviaties van het gemiddelde, etc.
Figuur 2, grafische weergave van een normaalverdeling, met op de x-as de Z-score.
Voorbeeld: je hebt met een peloton de pro-agility test gedaan, en wilt voor een deelnemer de Z-score berekenen. De gemiddelde tijd van het peloton was 5,16 seconden en de standaarddeviatie is 0,57 seconden. Een deelnemer had 4,92 seconden nodig om de pro-agility test af te ronden.
In andere bewoordingen betekent deze Z score dat deze deelnemers 0,42 standaarddeviatie eenheden onder het gemiddelde zit. In het geval van de pro-agility test betekent hoe minder tijd, hoe sneller de deelnemer is.
Grafieken kunnen het makkelijker maken om Z-scores overzichtelijk weer te geven en een vergelijking te geven van de verschillende fysieke capaciteiten van individuele militairen. Deze gegevens kunnen helpen bij het opstellen van een passend trainingsschema of opwerk traject, zie figuur 3.
Figuur 3, Z-scores voor een individu na een testafname met het peloton. De 0-lijn geeft het gemiddelde van het peloton aan.
Een andere manier om aan te geven hoe een individu scoort ten opzichte van andere test deelnemers is om een percentiel score aan te geven. Voorbeeld: een deelnemer behoort tot het 75e percentiel, dat wil zeggen dat 75% van de groep resultaten hadden die onder deze deelnemer scoren. Met een percentiel score is het dus mogelijk om individuele deelnemers te vergelijken met een normtabel van zijn of haar referentie groep. Zie ook tabel 1.
Samenvatting
In dit eerste artikel is gekeken op welke manieren resultaten van een (sport)motorische test kunnen worden omgezet in relevante informatie voor de sportinstructeur. Door een gemiddelde en standaarddeviatie te berekenen is de spreiding van de data inzichtelijk. Met een Z-score en percentiel score maakt het je mogelijk om een individuele sporter te vergelijken met een grotere groep.
In deel twee zal verder worden ingegaan op de vraag hoe trainingsdoelen kunnen worden gesteld aan de hand van de kleinste relatieve verandering. Daarnaast wordt het berekenen van een effect size uitgelegd en wat hier de meerwaarde van kan zijn.
Publicatiedatum: 04 juni 2021