STATISTIEK
METEN IS WETEN (deel 3)

Door Maarten Groot

In deel 1 van deze reeks is inzicht gegeven in enkele relevante beschrijvende statistieken zoals gemiddelde en de standaarddeviatie. In het tweede deel is ingegaan op de kleinst relevante verandering en effect size. In de voorgaande delen was ook te lezen welke formules passen bij beschrijvende en inferentiële statistiek. In dit deel hoop ik een brug te slaan tussen de theorie zoals de gegeven formules en hoe deze door middel van Excel 2016 kunnen worden gebruikt. In Excel zitten een groot aantal statistische bewerkingen in een aantal functies ingebouwd. Hierdoor kunnen grote aantallen berekeningen en bewerkingen tegelijkertijd worden uitgevoerd, wat veel werk en tijd scheelt en data snel om kan zetten in bruikbare informatie. 

Outliers
Voor er kan worden begonnen met bewerking van de verzamelde gegevens of data is het belangrijk deze te controleren op typfouten en extreme waardes, ook wel outliers genoemd. Deze controle kan gedaan worden door alle waardes één voor één na te lopen, maar sneller is het om Excel een boxplot met gegevens labels te laten maken. Ga hiervoor naar ‘Invoegen’ en druk vervolgens op de knop voor meer grafieken (rood omcirkeld in onderstaande afbeelding). 

Ga vervolgens naar de tab ‘alle grafieken’ en selecteer ‘Box en Whisker’. Druk op ‘OK’ en Excel maakt een boxplot. Vink vervolgens bij ‘GRAFIEKELEMENTEN’ ‘Gegevenslabels’ aan. In het voorbeeld hieronder is het vetpercentage van een groep militairen gemeten. Aan de resultaten heb ik het getal 5 toegevoegd als voorbeeld van een outlier. De getallen 13 en 24 zijn de minimale en maximale waarden die niet als outlier worden gezien. De getallen 13 en 18 geven het eerste en derde kwartiel aan. De “x” in het midden met daarachter het getal 15 geeft het gemiddelde aan. 

Nu bekend is dat deze data set een outlier heeft, kan worden gekeken waar dit aan ligt. Was dit bijvoorbeeld een typ fout en had dit bijvoorbeeld 15 moeten zijn? Of was er daadwerkelijk een deelnemer met zo’n afwijkend vetpercentage? In dat laatste geval kan je er voor kiezen de resultaten wel of niet mee te nemen. Het is belangrijk om te onthouden dat outliers van invloed zijn op de overige bewerkingen die je eventueel wilt gaan uitvoeren. Hoe kleiner de data set, hoe groter het effect van een outlier. 

Als de outliers zijn bekeken en er is besloten deze te gebruiken of niet, kan nog een laatste check worden uitgevoerd om te kijken of de data normaal is verdeeld, door het grafiek type te wijzigen in een histogram. 

Statistische functies
In het eerste deel van deze reeks was te zien hoe een normaal verdeelde data set er uit ziet. Nu bekend is dat onze data normaal verdeeld is, kan er een begin worden gemaakt met de statische bewerking van deze data.
Er zijn twee manieren om de functies in Excel te gebruiken. De eerste is door gebruik te maken van de formule ontwerp functie in Excel:

Onder de knop ‘meer functies’ staat een lijst met alle statistische functies. Selecteer hier de functie die je wilt gebruiken, zoals gemiddelde of standaarddeviatie en er opent een hulp venster waarin het programma stap voor stap aangeeft welke gegevens ingevoerd moeten worden om de functie te gebruiken.

Syntax
De tweede manier, die de meeste die hard Excel gebruikers toepassen, is door te werken met een syntax. Met deze manier selecteert de gebruiker een cel waarin is resultaat van een formule moet komen, zoals het gemiddelde of een som. Een syntax begint altijd met ‘=’.
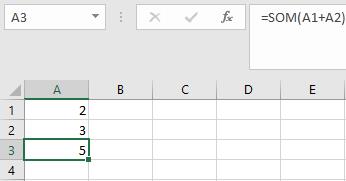
Wil je bijvoorbeeld Excel een som laten uitrekenen dan kan dat door de volgende syntax op te stellen: =SOM(A1+A2)

In het voorbeeld hiernaast is te zien dat met deze syntax de waarde van cel A1 bij cel A2 wordt opgeteld en het antwoord hiervan wordt in cel A3 gegeven.
Op deze manier kan een groot aantal functies worden gebruikt. In tabel 1 een overzicht van een aantal relevante functies en de syntax hiervoor.

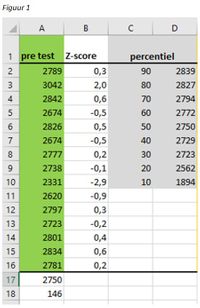
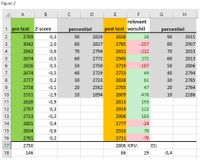
Praktijk voorbeeld: Een groep van 15 leerlingen in de AMOL legt in opleidingsweek 1 de 12 minuten loop af. De resultaten hiervan zijn terug te vinden in figuur 1, kolom A, met groene achtergrond.

In cel A17 is het gemiddelde berekend met de syntax =GEMIDDELDE(A2:A16). In cel A18 is de standaarddeviatie berekend met de syntax =STDEV.P(A2:A16). Vervolgens is voor elke deelnemer in kolom B de Z-score berekend met de syntax =SOM(A2-$A$17)/$A$18. In deze syntax is voor cel A2 de Z score berekend door de waarde in A2 van het gemiddelde af te trekken en de uitkomst daarvan door de standaarddeviatie. Het “$” is gebruikt om  het gebruik van een cel vast te zetten. Hierdoor kan een functie makkelijk gekopieerd worden. In kolom C en D is een tabel gemaakt met de percentielscore. Hiervoor is de syntax =PERCENTIEL(A2:A16;SOM(C2/100)) gebruikt. Deze syntax laat zien dat het mogelijk is om meerdere functies in een te combineren, zo is er een SOM functie in de vorige syntax ‘genest’.

Na 12 weken leggen de 15 AMOL leerlingen opnieuw de 12 minuten loop af. De resultaten hiervan zijn in figuur 2 terug te vinden in kolom E, met oranje achtergrond. 

Opnieuw zijn van deze resultaten het gemiddelde en de standaarddeviatie berekend in cel E17 en E18. Om er achter te komen of deze verschillen tussen pre- en post test werden veroorzaakt door toeval of echt relevant waren, is in cel F18 de Kleinst Relevante Verandering (KRV) berekend met de functie =SOM(0,2*A18).

Vervolgens is in kolom F voor elke leerling het verschil tussen de pre- en post test berekend. Met de functie ‘Voorwaardelijke opmaak’ is aangegeven dat de waarde in kolom F  kleiner dan (<) de waarde in cel F18 rood dient te worden gearceerd. Met dezelfde functie is ook aangegeven dat de waarde groter dan (>) de waarde in cel F18 groen dient te worden gearceerd.

Percentielen voor de post test zijn opgemaakt met dezelfde functie als de percentielen voor de pre test. Opvallend detail hierin is dat de percentiel waarden in de tabel voor de post test hoger liggen dan de waarden in de pre test. Dit wijst er op dat het uithoudingsvermogen van deze groep is toegenomen. Om dit trainingseffect beter inzichtelijk te maken, is de Effect Size berekend met de syntax: =SOM((E17-A17)/A18). De uitkomst hiervan is 0,4. In het tweede deel van deze reeks is aangegeven dat een ES van 0,2 en 0,6 klein en matig zijn. Het effect van deze trainingsperiode was dus tussen klein en matig in, dit geeft mogelijk aanleiding om nog eens kritisch terug te kijken naar het trainingsprogramma. Aan de andere kant is op te merken dat een man van onder de 30 jaar, gemiddeld 2460 meter loopt in 12 minuten. Daarmee heeft deze trainingsgroep met een gemiddelde afstand van 2806 meter al een zeer goed uithoudingsvermogen en zorgt ook mogelijk de wet van verminderde meeropbrengst voor deze kleine ES.

Samenvatting

In deze reeks is aangegeven hoe statistiek de sportinstructeur kan ondersteunen in het vaststellen van een beginsituatie, het stellen van doelen voor de komende trainingsperiode, het beoordelen van de vooruitgang van de leerlingen en het evalueren van de effectiviteit van het aangeboden trainingsprogramma. In dit laatste deel zijn een paar praktische voorbeelden gegeven van functies in Excel 2016 die kunnen ondersteunen in het toepassen van statistiek.

Publicatiedatum: 02 juli 2021